大数の法則は、簡単な例で説明すればサイコロをn回振って1が出る割合が、nが大きくなれば理論的な期待値1/6に近づくというものです。統計学の教科書に必ず載っていますが、証明まで載せている本は意外と少ないです。統計学の中心的な定理なのに、不思議です。一体どの教科書になら証明まで載っているんだろうと思ってたら、小谷 眞一『測度と確率』という本にありました。統計の本ではなく確率論の本には証明まできっちりと示しているということなのでしょうか。
初学者にとって少し混乱しやすいのではないかと思えることは、大数の法則には大数の弱法則と大数の強法則の2つがあり、書物によっては、大数の弱法則のことを大数の法則と呼んでいたり、大数の強法則のことを大数の法則と呼んでいたりすることです。大数の弱法則はチェビシェフの不等式を用いると比較的容易く示せることから、大数の弱法則は証明まで含めて紹介されていることが多いみたいです。
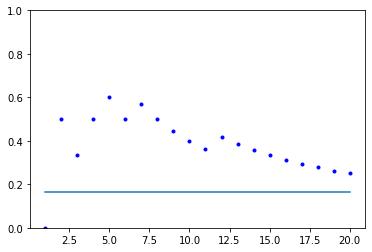
さて、大きな数(large number)といってもどれくらいの数のことを言うのでしょう?100?1000?試してみます。まずは、サイコロを20回振ってみます。
サイコロを振った回数: 20 回
出た目:3 1 5 1 1 5 1 3 6 5 4 1 6 3 2 2 5 2 4 4
1の目がでた回数: 5 回
1の目がでた割合:0.25
サイコロを振った回数ごとに、それまでに1が出た割合をグラフにすると、下のようになります。最初は0ではなかったので、0/1、次に1の目がでたので、1/2。4回目にまた1が出たので、2/4。5回目にも1の目が出たので、3/5=0.6と言った調子です。1が出ない回が続けば、この割合は減少します。グラフ内の直線は理論的な期待値すなわち、1/6 = 0.1666…
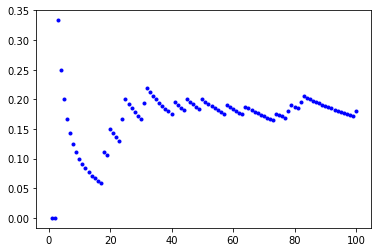
サイコロを振って1が出る確率は1/6 = 1.666666… ですが、100回振ったらどんな感じでしょうか?
サイコロを100回振った結果:5516534665224554215166211443441152254563135214636124433351532341463436365142611551145255535244526461
1が出た割合:1.8
100回だと全然近くないですね。1000回サイコロを振ってみると、
サイコロを1000回振った結果:5261646223634322633256613124434366551646321553343646135426131434625443422664254561323434654124546123566446614643131421224435636332555342532253134665645536643146666326561543163251635543516213244243655244616623245145666345662221164656644561456663146552415151634646643553234136142365232332155415565656662352432423654451451132243133435131326155261131621555124432621546214231544121241245155255356511163512613641531546422451332335625434466132646633463662323526666126622243162616261113244463223255233644423151154664516136266434246513215226565636214416316224261266436445351266145616525433126135235512646222455616451633224653223611664614316115113654345321464126515364415432544322461165426443413451653213165341635343654614526411221352556456562251624466313664122515111562653625451225465141416431333446434652252424561411311226551454325332614136122433114312553152666425611142322226361441616564151133234611312411362154241542163552551263151341665151364651513114453151531315514123364363614322445652563322121352513355
1が出た割合:1.73
1000回でも全然大きい数とはいえないようです。
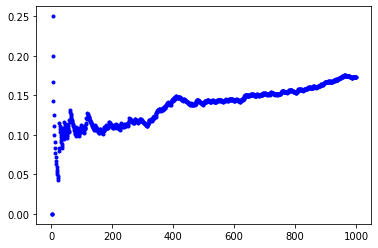
1万回⇒0.1648
 このグラフ作成時は10000回で、1が出た割合は、0.162と言う値でした。
このグラフ作成時は10000回で、1が出た割合は、0.162と言う値でした。
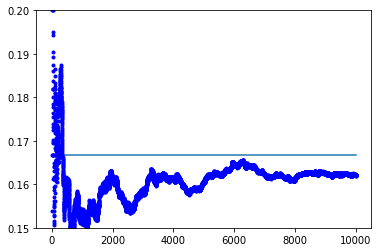
10万回⇒0.16652 0.1682 0.16729 0.16715 0.16662 (5回試した結果)
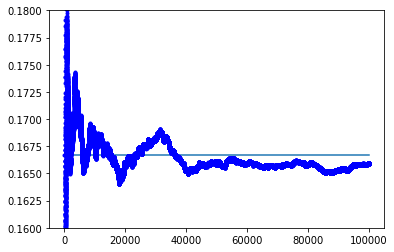 このグラフの例だと1が出た割合は、0.1659でした。グラフ中の直線は、y=1/6の位置を示します。
このグラフの例だと1が出た割合は、0.1659でした。グラフ中の直線は、y=1/6の位置を示します。
もちろん、試すごとにサイコロの目の出方は変わるのでどれくらい近くなるかも変わるのですが、およその感じはつかめると思います。10万回サイコロを振ってようやくそれらしい近づき方をしてきました。といっても2~3桁の精度。
100万回⇒0.166157
1000万回⇒0.1664854
 このグラフの例だと、サイコロを1千万回振って、1の目がでた回数は1666577回、すなわち割合でいうと0.1666577でした。
このグラフの例だと、サイコロを1千万回振って、1の目がでた回数は1666577回、すなわち割合でいうと0.1666577でした。
1億回⇒0.16667195 0.16669191 0.16671321 0.16668115(4回試した結果)
サイコロを1億回ふってようやく4~5桁の精度です。
ちなみにサイコロを振るといっても、本物のサイコロを10万回振るわけにはいかないので、pythonの乱数発生機能を使っています。1が出た割合を毎回forループでまわして計算すると、nが大きくなると時間がかかりすぎます。pythonだとnumpy配列を使えば、n=1億でも一瞬で計算してくれました。
描画に使ったpython3のコード
# forループを使わ宇にnumpy配列を使って計算すると速い!
import numpy as np
import matplotlib.pyplot as pltn = 20#1億回は描画に時間がかかっていて諦めた。100万回なら描画も数秒もかからなかった。
print(‘サイコロを振った回数:’,n)
trial = list(range(1,n+1))# 1からnまでのリストX = np.random.randint(1,7,n)#さいころをn回ふる
print(‘X:’,X)
Sn = np.count_nonzero(X == 1)
print(‘1の目がでた回数:’,Sn)
A = Sn/n
print(A)
X_1 = X==1#さいころの目が1かどうか
# print(‘X_1:’,X_1)S =np.cumsum(X_1==True) /trial#リストの要素ごとの除算 cumsumは要素の累積和
# print(‘S:’,S)#基準の線の描画
plt.plot([1,n], [1/6, 1/6])#大数の法則の描画
plt.plot(trial,S,’.b’)
# plt.ylim(0.165, 0.17)
plt.ylim(0,1)
大数の弱法則と大数の強法則のそれぞれについて証明が紹介されている確率論の教科書として、小谷 眞一『測度と確率』があります。大数の弱法則のほうはチェビシェフの不等式を使って簡単に証明ができるため、ほとんどの数理統計学の本で説明がなされているみたいです。