階乗は、例えば５の階乗なら５ｘ４ｘ３ｘ２ｘ１＝120、6の階乗なら６ｘ５ｘ４ｘ３ｘ２ｘ１＝720と言った具合で、一つずつ少ない数を掛けていったものです。記法はビックリマーク使い、5!＝120のように書きます。

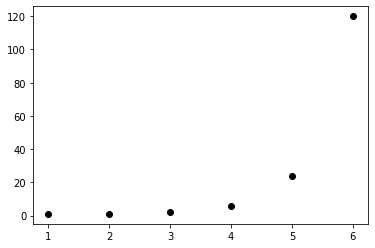
1! =1, 2!=2, 3!=6, 4!=24, 5!=120, 6!=720, 7!=5040と急激に増加していきます。

グラフに描いてみると、

となります。正の整数ごとに計算してプロットしたわけですが、これを見ていると、なんだか各点をスムーズにつないでみたくなります。

2.5の階乗はいくつでしょう？4.1の階乗は？階乗の定義上、自然数に対してしか階乗は定義されていないわけですが、どういう関数ならもとの階乗の値にも一致し、なおかつ途中をもきれいにつないでくれるのでしょうか。階乗を正の整数だけでなく、実数、さらには複素数にまで拡張したものがガンマ関数と呼ばれるものです。ガンマ関数を考えついた人は、あの有名な数学者オイラー(Euler)でした。

When Euler arrived in St. Petersburg in 1728, Daniel Bernoulli and Christian Goldbach were already working on problems in the “interpolation of sequences.” Their problem was to find a formula that “naturally expressed” a sequence of numbers.

Bernoulli and Goldbach were stumped trying to interpolate two particular sequences. The first was the sequence we now call the factorial numbers, 1, 2, 6, 24, 120, 720, etc. They called it the “hypergeometric progression.”

Euler announced his solution in a letter to Christian Goldbach dated October 13, 1729.

Euler’s exposition in the letter of October 1729 is very brief, but he gave more details and consequences in an article, De progressionibus transcendentibus, seu quarum termini generales algebraice dari nequeunt, “On transcendental progressions, or those for which the general term is not given algebraically.”

Euler, Leonhard, De progressionibus transcendentibus, seu quarum termini generales algebraice dari nequeunt. Commentarii academiae scientiarum imperialis Petropolitanae 5 (1730/31) 1738, pp. 36-57. Reprinted in Opera omnia I.14, pp. 1-24. Original Latin and an English translation by Stacy Langton are available at EulerArchive.org.

（引用元：How Euler Did It by Ed Sandifer Gamma the function September 2007）

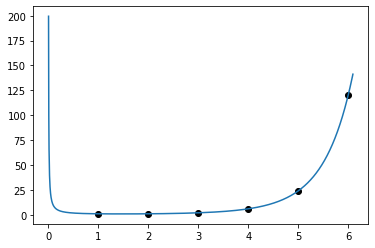
さてオイラーが定義したガンマ関数のせきぶんの公式を使って計算（ウソ、pythonのガンマ関数で算出）してグラフを描いてみると、

こんな曲線になりました。階乗の定義による値はきれいに通っていますが、０に近いところでとんでもない挙動を示しています。正の整数が引数の場合は、Γ(6)=5! と、一つ小さい数の階乗になります。Γ(1)=0!なのですが、Γ(0)は値がないのです。負の実数でもガンマ関数は計算されますが、負の整数は値がありません。負の数までぷろっとすると、もっと不思議なグラフになります。階乗は26の階乗でも、26!=6.2×10^23と、アボガドロ数と同じ程度の大きさにもなります。階乗って凄い！

ちなみにｘ軸の刻みは0.001で描画しています。ｙ軸は対数表示。

コンピューターが無い時代は大変だったと思いますが、関数の式をみてもイメージが湧かなければこうしてpythonなどのプログラミング言語を使えば簡単にグラフを描けてしまうので、pythonさまさまです。

キーワード：ガンマ関数 証明　ガンマ関数 積分　ガンマ関数 例題　ガンマ関数 収束　ガンマ関数 性質　ガンマ関数 計算