実験で得られたデータに意味があるのかないのかを調べるとき、統計学的な検定を行います。例えばある遺伝子を破壊したマウス20匹と(実験群)と野生型マウス20匹(対照群)から何かの値を測定したとき、実験群から得られた20個の測定値の平均値と対照群から得られた平均値との間に差があるかどうか。差があることを期待したとして、実際に差が少し数字上あったとして、その差が「有意差」なのかどうか。
ステップ1:帰無仮説 差がない を設定 (対立仮説は、 差がある)
ステップ2:有意水準(稀すぎるので帰無仮説を棄却するための基準の値) 5% と設定
ステップ3:(確率密度変数、すなわち確率変数の分布が既知の)検定統計量(test statistic)を計算
ステップ4:その統計量の値が得られる確率を計算し 有意水準より小さければ 帰無仮説を棄却し、対立仮説を採用する。有意水準と同じかそれより多きければ、差があるとはいえない(差がないとも言えない)。
ステップ1,2,4は基本的にどんな検定でも共通なので、ステップ3が一番重要といえます。例えば、検定統計量tならt分布に従います。検定統計量カイ2乗は、カイ2乗分布に従います。検定統計量FならF分布に従います。検定量や分布は、検定の種類によって異なりますが、上記の1から4までのステップはなんであっても同じです。
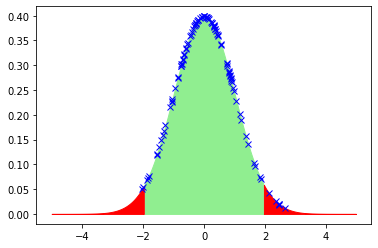
下のグラフは標準正規分布(平均値=0,標準偏差=1)ですが、棄却域(左側2.5%、右側2.5%、合わせて5%)がわかるように赤色にしてあります。確率密度関数の面積が確率を表しています。一回の研究で有意差の有無を検定したら、検定統計量を一つ計算して、このグラフのどこに来るかを調べるわけです。標準正規分布の場合、X=-0.96から0.96の間の数字は95%の確率で生じます。棄却域(-0.96未満または0.96より大きい数)の値が得られる確率は5%未満なので、稀にしか起こらない、すなわち帰無仮説は正しくなかろうから対立仮説を採用することになります。0に近い値がでやすいということを実際に標準正規分布に従う乱数発生により確かめてみました。100個の乱数を発生させて、xを描いてあります。「100個の乱数の発生」を何回かやるとそのたびごとに得られるxの値は違っていますが、下図は一例ですが、棄却域で得られたのは7回でした。棄却域に値を得ることが、稀であることがわかります。
参考
- 自分が受けた講義のノート
- 準1級対応 統計学実践ワークブック 第10章 検定の基礎と検定法の導出
- 4Stepエクセル統計 第4版 (2015年)